Bất kì một lập trình viên nào đều từng thao tác với cơ sở dữ liệu. Và cụ thể hơn là các query truy vấn, đánh index cho dữ liệu. Nhưng đằng sau việc đánh index đó thì điều gì xảy ra? Trong bài vết này sẽ giới thiệu tới một thuật toán là Roaring Bitmap được giới thiệu năm 2016. Đây một thuật toán giúp tăng tốc rất nhiều việc thực hiện phép tính và nén bitmap.
Bài viết dưới đây dựa vào nội dung từ paper “Better bitmap performance with Roaring bitmaps”, các bạn có thể xem bản gốc chi tiết tại https://arxiv.org/abs/1402.6407 hoặc từ trang chủ của nó tại: https://arxiv.org/abs/1402.6407.
Đầu tiên chúng ta đi tìm hiểu về khái niệm Bitmap. Khái niệm này là phần quan trọng nhất chúng ta cần nắm được trước khi đi guyên, S.
Một Bitmap – hay có thể hiểu là một tập hợp các bit. Nó là một mảng nhị phân biểu diễn nhỏ gọn hiệu quả cho tập số nguyên S.
Trong 1 bitmap gồm n bit, bit thứ i là 1 nếu số nguyên thứ i nằm trong phạm vi [0 -> n-1] và tồn tại trong tập hợp. Bitmap trong java được thể hiện thông qua một class là Bitset.
Ví dụ:
Tập {3,4,7} có thể biểu diễn là 10011000 . Còn tập {4, 5, 7} có thể biểu diễn là 10110000.
Các bit ở vị trí 3, 4, 7 hoặc 4, 5, 7 được đánh số 1, ngược lại là 0.
Hãy thử nghĩ, nếu tập chỉ có 1 số và số đó rất lớn thì sẽ như thế nào? Ví dụ số 1000, thì chuỗi bit nhị phân của bạn cũng sẽ gồm rất nhiều bit. Và đây chính là bài toán mà các thuật toán của chúng ta sẽ giải quyết.
Bitmap còn có tên gọi khác là Bit Array hay Bitmap Index. Như vậy có nghĩa là Bitmap cũng chính là Bitmap Index. Tiếp đến chúng ta sẽ xem Bitmap dùng ở đâu trong cơ sở dữ liệu?
Chúng ta cùng xem xét ví dụ dưới đây:
Trong ví dụ dưới đây là đang đánh index cho trường HasInternet, và loại index được sử dụng là Bitmap. Ngoài Bitmap Index, chúng ta còn có B-Tree và Hash. Bitmap Index thì bạn có thể tìm thấy trong Oracle. Nếu sử dụng MySQL thì bạn sẽ chỉ thấy B-Tree và Hash mà thôi.
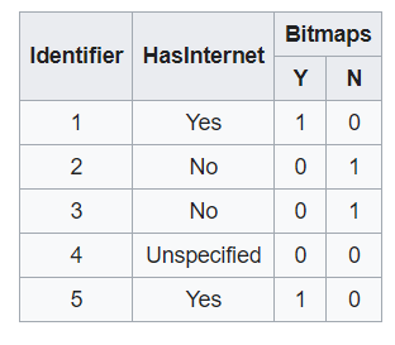
Ta thấy, trường HasInternet xảy ra ba trường hợp sau:
+ Yes thì giá trị Bitmap sẽ là 1 0.
+ No là 0 1.
+ Không xác định là 0 0.
Chú ý rằng mỗi cấu trúc lưu trữ Bitmap Index này sẽ gắn với 1 Identifier. Chỉ số này sẽ liên kết với dữ liệu gốc ban đầu để lấy thấy tin khi truy vấn.
Cụ thể Bitmap Index được vận hành như thế nào, ta cùng xem nhé.
Một lưu ý là chỉ mục Bitmap hiệu quả nhất đối với các query chứa điều kiện where. Các hàng thỏa mãn một số điều kiện nhưng không phải tất cả điều kiện đều được lọc ra trước khi bảng đó được truy cập. Điều này sẽ cải thiện khá nhiều thời gian phản hồi.
Chỉ mục Bitmap không phù hợp với các ứng dụng xử lý giao dịch trực tuyến (OLTP applications). Các ứng dụng này thường có số lượng lớn các giao dịch đồng thời sửa dữ liệu. Các chỉ mục này thường hỗ trợ việc quyết định trong các ứng dụng lưu trữ dữ liệu nơi mà người dùng thường truy vấn dữ liệu hơn là cập nhật dữ liệu. Ưu điểm của việc sử dụng chỉ mục Bitmap là lớn nhất đối với số lượng giá trị khác biệt là nhỏ so với số hàng trong bảng. (Hay nói cách khác đó là Cardinality nhỏ)
Ví dụ với 1 bảng có 1 triệu hàng với 10.000 giá trị khác nhau là hợp lý cho việc lựa chọn Bitmap index.
Các điều kiện AND và OR trong mệnh đề Where có thể được giải quyết nhanh chóng bằng các phép toán xử lý bit tương ứng trên các bitmap trước khi chuyển đổi kết quả từ phép tính đó thành rowid.
Nếu số lượng kết quả là nhỏ, truy vấn sẽ thực hiện rất nhanh chóng mà không cần dùng đến việc quét toàn bộ bảng
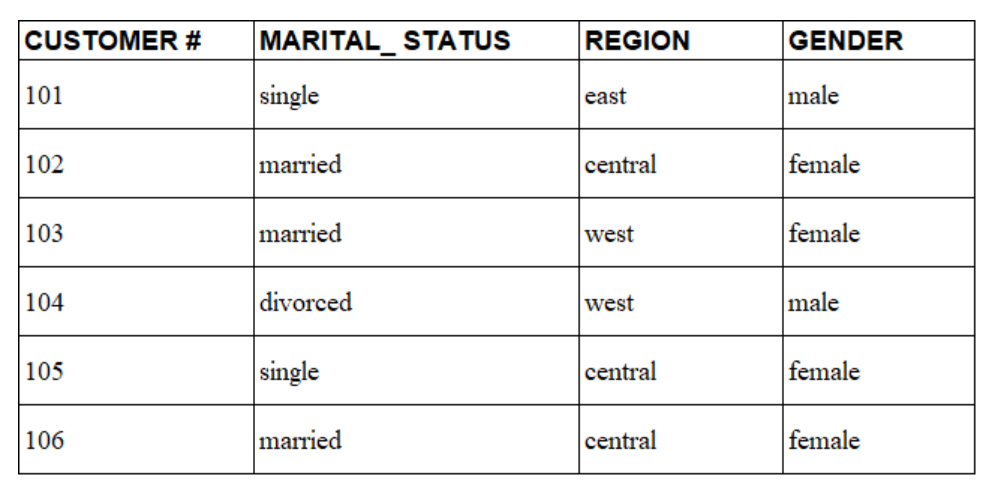
Các cột Marital_status, Region, Gender, Income_level với Lượng số là thấp, phù hợp với việc sử dụng Bitmap index.
Lượng số (Cardinality) là số lượng phận tử khác nhau trong 1 tệp. Các bạn có thể xem thêm về Cardinality trên wiki.
Minh họa với cột Region thì có dạng như sau:
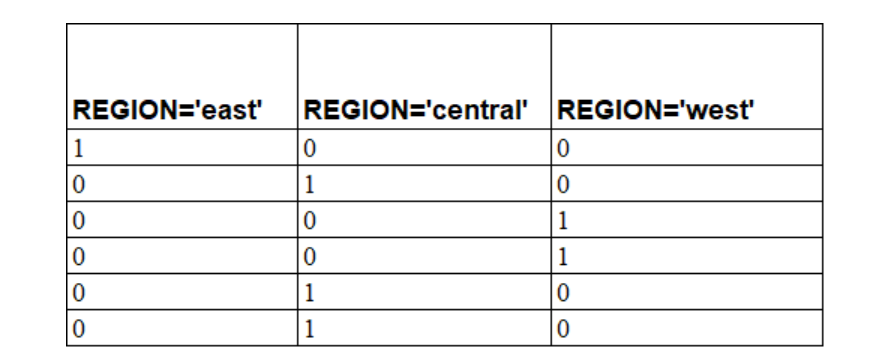
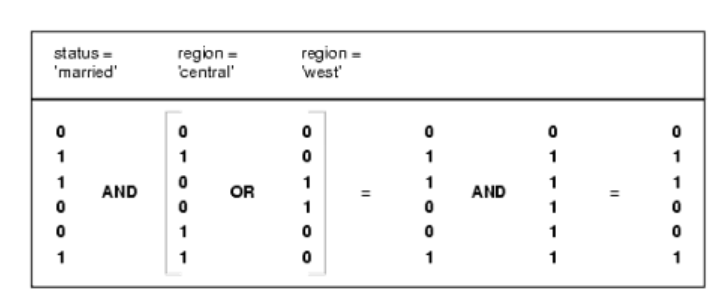
Ví dụ chúng ta có câu hỏi cần xử lý:
Có bao nhiêu khách hàng đã kết hôn và ở center hoặc west sẽ là:
SELECT COUNT(*) FROM customer WHERE MARITAL_STATUS = ’married’ AND REGION IN (’central’,’west’);
Các chỉ mục bitmap có thể xử lý truy vấn này với hiệu quả cao chỉ bằng cách đếm số lượng các chỉ mục trong bitmap kết quả, từ đó sẽ truy cập và lấy ra dữ liệu cần thiết từ bảng lưu trữ.
Theo dòng lịch sử có rất nhiều thuật toán nén bitmap được ra đời, sơ lược được tổng kết trong hình vẽ như sau

Chúng ta sẽ tìm hiểu về 2 thuật toán khá tiêu biểu đó là WAH, và CONCISE. Trong đó Concise là một thuật toán khá ưu tú, các bạn có thể đọc thêm trong bài báo cáo khoa học sau https://arxiv.org/abs/1004.0403
WAH (Word-Aligned Hybrid) là một thuật toán nén bitmap cổ điển. Nó phân vùng một bitmap không nén (đầu vào) thành các nhóm trong đó mỗi nhóm chứa 31 bit. Nó phân loại vào 2 nhóm là fill group và literal group. Một nhóm được gọi là fill group nếu tất cả các bit trong nhóm đó đều giống hệt nhau.
Ví dụ như là 0000000000000000000000000000000 (hay là 031) thì được gọi là fill group. Nếu toàn bộ các bit là 1 thì gọi là 1-fill group, ngược lại nếu toàn bộ các bit là 0 thì gọi là 0-fill group.
Các nhóm được gọi là literal group nếu trong nhóm đó chứa cả các bit 0 và 1. Thuật toán nén WAH chỉ nén các fill-group, WAH có thể nén 1 chuỗi các fill-group liền nhau. Trong đó bit đầu tiên là 1 để biểu thị cho biết đây là fill group. Bit thứ 2 có thể là 0 hoặc 1 để biểu thị cho biết đây là 1-fill group hay 0-fill group. 30 bit tiếp theo để biểu thị cho số lượng các nhóm fill group. WAH mã hóa literal group bằng cách sử
dụng 1 word (32 bit), trong đó bit đầu là 0 và 31 bit sau là dữ liệu của literal group đó.
Ví dụ:
Mình khá là lười gõ lại latex nên xin phép gõ dưới dạng hơi nông dân như dưới đây.
Cho Bitmap 160 bits:1 0^20 1^3 0^111 1^25 (có nghĩa là bit 1 sau đó có 20 bit 0, 3 bit 1, 111 bit 0 và 25 bit 1) thì WAH chia vào 6 nhóm như sau
G1(1 0^20 1^3 0^7); G2(0^31); G3(0^31); G4(0^31); G5(0^11 1^20); G6(0^26 1^5) và sau khi mã hóa sẽ là G1(0 1 0^20 1^3 0^7),
G2 G3 G4 sẽ được gộp lại là (1 0 0^22 011) G5(0 0^11 1^20); G6(0 0^26 1^5).
CONCISE (Nén N bộ số nguyên vào có thể dùng 1 lần – Compressed N Composable Integer Set) là giải pháp được đề xuất để cải thiện WAH. Nó giải quyết một hạn chế của WAH là nếu một literal group chỉ có một bit khác với fill-group tiếp theo, thì WAH vẫn sử dụng một word đầy đủ để lưu trữ literal group.
Ngược lại, CONCISE lưu trữ fill group hỗn hợp với fill group tiếp theo với nhau bằng cách lưu trữ vị trí của bit lẻ. CONCISE phân vùng bitmap không nén (dữ liệu vào) thành các nhóm 31 bit. Nó sử dụng một word để đại diện cho một literal group bằng cách đặt bit đầu tiên thành 1 và 31 bit còn lại bằng cách sao chép thông tin từ literal group xuống.
CONCISE cũng sử dụng một word để đại diện cho một loạt các fill group. Nó chứa các thông tin sau. Bit đầu tiên được đặt bằng 0. Bit thứ 2 cho biết loại fill group nào (0-fill group hoặc 1-fill group). 5 bit sau lưu trữ vị trí của bit lẻ, chúng là 00000 nếu không có bit lẻ nào. 25 bit còn lại lưu trữ số các fill group trừ đi một.
Cho 1 bitmap 160 bit 0^23 1 0^111 1^25 thì Consise sẽ phân thành các nhóm: G1(0^23 1 0^7), G2(0^31); G3(0^31); G4(0^31);
G5(0^11 1^20); G6(0^26 1^5) sau khi mã hóa sẽ là từ G1 tới G4 sẽ là (0 0 00111 0^23 11) , G5 là (1 0^11 1^20), G6 là (1 0^26 1^5).
Còn rất nhiều thuật toán nén bitmap khác có thể kể đến như là: BBC, EWAH, PLWAH, VALWAH. . . tuy vậy đa phần các thuật toán nén bitmap này đều dựa trên RLE. Trong khuôn khổ bài viết này Code Tu Tam sẽ không đề cập chi tiết tới các thuật toán này.
Có thể xem qua lược đồ đơn giản sau:

Bitmap Index đã được áp dụng rộng rãi trong các hệ thống cơ sở dữ liệu hiện đại bao gồm lưu trữ theo hàng và cột, ví dụ: PostgreSQL, Microsoft SQL Server, Oracle, MonetDB, C-store, Vertica và Apache Hive. Theo như thông tin chia sẻ trên website roaringbitmap.org thì Roaring Bitmap được sử dụng trong các nền tảng như là: Elasticsearch, Apache Spark, Netflix’s Atlas, LinkedIn’s Pivot, Metamarkets’ Druid, Pilosa, Apache Hive, Apache Tez, Microsoft Visual Studio Team Services…
Trong phần tiếp theo chúng ta sẽ tìm hiểu về Roaring Bitmap và so sánh Roaring Bitmap với thuật toán Concise và Wah. Ngoài ra sẽ có mã nguồn chương trình chạy thử đi kèm. Hãy like và share bài viết để ủng hộ Code Từ Tâm bạn nhé!
Bình luận: