Trong phần trước chúng ta đã tìm hiểu về Bitmap cũng như một số thuật toán nén cơ bản. Trong bài viết này, chúng ta cùng tìm hiểu chi tiết về Roaring bitmap và so sánh tốc độ thực thi của Roaring Bitmap với các thuật toán khác. Kiến thức trong bài viết dựa trên thu thập và đúc kết từ nhiều nguồn khác nhau, do vậy không tránh khỏi sai sót mong các bạn góp ý giúp Code Tu Tam.
Roaring là một phương pháp nén bitmap kết hợp (hybrid compression) và nó không dựa trên thuật toán nén dữ liệu hàng loạt (RLE). Roaring phân vùng dữ liệu [0, n) (n < 232) thành các nhóm khác nhau với phạm vi 216, trong đó tất cả các phần tử trong cùng một đoạn chia sẻ cùng 16 bit quan trọng nhất.
Ví dụ: ba nhóm đầu tiên quản lý các phạm vi sau: [0 ∼ 65535], [65536 ∼ 65536 × 2 − 1] và [65536 × 2 ∼ 65536 × 3 − 1]. Roaring mã hóa một đoạn tùy thuộc vào số lượng phần tử thực tế (k) trong đoạn đó.
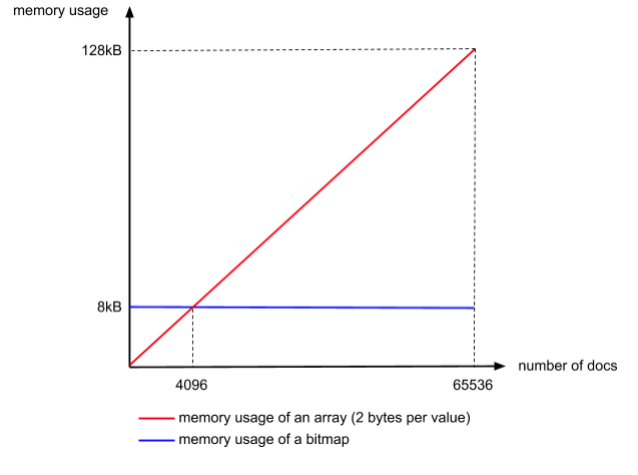
Nếu k > 4096 Roaring sử dụng bitmap 65536 bit (không nén) để mã hóa các phần tử.
Mặt khác, nó sử dụng một mảng được sắp xếp gồm các số nguyên 16 bit. Roaring chọn 4096 làm ngưỡng vì nó đảm bảo rằng mỗi số nguyên sử dụng không quá 16 bit để biểu diễn, cụ thể hơn là vì Roaring sử dụng 65536 bit để đại diện cho 4096 số nguyên với nhiều nhất là 16 bit cho 1 số nguyên trong mảng.
Lưu ý rằng, Roaring không cần phải lưu trữ nhiều hơn 16 bit cho tất cả các phần tử trong cùng một nhóm vì chúng giống nhau. Do đó, Roaring là một phương pháp nén kết hợp kết hợp danh sách số nguyên (16-bit) không nén và bitmap không nén.
Roaring cũng hỗ trợ phép giao (AND) và phép hợp (OR) trực tiếp trên các bitmap được nén. Trong mỗi vòng, nó giao (hoặc hợp) hai nhóm từ các bitmap khác nhau theo 1 trong bốn cách như sau: bitmap với bitmap, bitmap với array, array và bitmap và array và array.
Roaring Bitmap phân vùng phạm vi chỉ mục 32-bit ([0, n)) thành các phần của 216 số nguyên có cùng 16 chữ số có nghĩa nhất. Nó tạo ra các container để lưu trữ 16 bit ít quan trọng nhất của chúng.
Khi một đoạn chứa ít hơn 4096 số nguyên, chúng sử dụng một mảng được sắp xếp gồm các số nguyên 16 bit được đóng gói. Khi có hơn 4096 số nguyên, chúng sử dụng 1 bitmap 2
16 bit. Do đó, Roaring Bimap sẽ có 2 loại container khác nhau: một array container cho các phần thưa thớt và một bitmap container cho các phần dày đặc.
Ngưỡng 4096 đảm bảo rằng ở cấp độ của container, mỗi số nguyên sử dụng không quá 16 bit (Lớn hơn con số này là 1 Bitmap – có hiệu quả sử dụng tốt hơn một mảng).
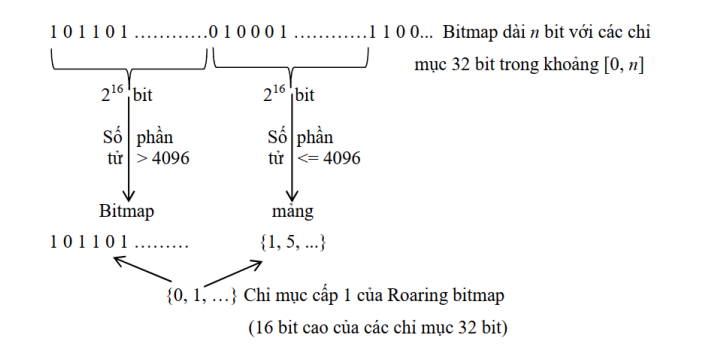
Các container chứa trong 1 mảng động với 16 bit quan trọng nhất: điều này giống như là 1 chỉ mục cấp 1. Mảng này giữ cho các container sắp xếp theo 16 bit quan trọng đó. Chúng kỳ vọng chỉ mục cấp đầu tiên này thường nhỏ: khi n = 1.000.000, nó chứa nhiều nhất 16 mục. Vì vậy, nó thường phải nằm trong bộ nhớ cache của CPU. Bản thân các container không bao giờ được sử dụng nhiều hơn 8 kB.
Để minh họa cấu trúc dữ liệu, hãy xem xét danh sách 1000 bội số đầu tiên của 62, tất cả các số nguyên [216, 216 + 100) và tất cả các số chẵn trong [2 × 216, 3 × 216). Ở định dạng Roaring, tất cả bội số của 62 và các số nguyên trong [216, 216 + 100) được lưu trữ bằng cách sử dụng một array container 16-bit/số nguyên. Thậm chí số trong [2 × 216, 3 × 216) được lưu trữ trong một Bitmap container 16 bit.
Mỗi Roaring container theo dõi lượng số của nó bằng cách sử dụng 1 bộ đếm. Như vậy việc tính toán lượng số của 1 Roaring Bitmap có thể rất nhanh: nó sử dụng tối đa là n/216 biến đếm.
Để kiểm tra sự hiện diện của một số nguyên 32 bit x, đầu tiên chúng ta tìm kiếm container tương ứng với x/216, sử dụng tìm kiếm nhị phân. Nếu một container bitmap được tìm thấy, chúng ta truy cập bit thứ x mod 216. Nếu một container mảng được tìm thấy, chúng ta tiếp tục tìm kiếm nhị phân một lần nữa.
Tương tự, khi chúng ta thêm hoặc loại bỏ một số nguyên x, đầu tiên chúng ta tìm container tương ứng. Nếu container được tìm thấy là bitmap, chúng ta thiết lập giá trị của bit tương ứng và cập nhật số phần tử của nó. Ngược lại, chúng ta sử dụng tìm kiếm nhị phân rồi thêm hoặc xóa tuyến tính (linear-time).
Khi loại bỏ một số nguyên, một container bitmap có thể trở thành một container mảng nếu số phần tử của nó chưa vượt quá 4096. Khi thêm một số nguyên, một container mảng có thể trở thành một container bitmap khi số phần tử của nó vượt quá 4096. Khi điều này xảy ra, một container mới được tạo ra chứa dữ liệu được cập nhật trong khi container cũ được bỏ đi. Chuyển đổi một container mảng thành một container bitmap được thực hiện bằng cách tạo một container bitmap mới với giá trị khởi tạo là các bit 0 rồi thiết lập các bit tương ứng. Để chuyển đổi một container bitmap thành một container mảng, chúng ta trích ra vị trí của các bit 1 sử dụng thuật toán 2.
Các phép toán logic được đề cập tới là phép nối (OR) và giao (AND).
Một hoạt động với bit giữa hai bitmap roaring bao gồm lặp lại và so sánh 16 số nguyên bit cao trên các chỉ mục cấp 1.
Các mảng đã sắp xếp cấp 1 cho phép thực hiện so sánh với độ khó là O(n1 + n2) trong đó n1 và n2 là độ dài tương ứng của hai mảng được so sánh. Một Container có thể biểu diễn bởi 2 cấu trúc dữ liệu khác nhau là Bitmap hoặc Array.
Mảng cấp một được sắp xếp cho phép so sánh cấp một trong thời gian O(n1 + n2), trong đó n1 và n2 là độ dài tương ứng của hai mảng được so sánh. Thuật toán cũng duy trì các vùng chứa mảng được sắp xếp để có những lợi thế tương tự. Vì vùng chứa có thể được biểu diễn bằng hai cấu trúc dữ liệu khác nhau, bitmap và mảng, nên sự kết hợp logic hoặc giao cắt giữa hai vùng chứa liên quan đến một trong ba trường hợp sau:
Bitmap với Bitmap: We iterate over 1024 64-bit words. For unions, we perform 1024 bitwise ORs and write the result to a new bitmap container. Xem thuật toán 1

Đối với phép giao thì ta tính toán lượng số của kết quả, sử dụng 1024 phép tính bit AND. Nếu lượng số lớn hơn 4096, thì chúng ta tiến hành như với phép hợp, ghi kết quả của các phép tính bit AND này vào một Container Bitmap mới. Ngược lại, chúng ta sẽ tạo một Container mảng
Trọng số Hamming của một dãy ký tự là khoảng cách Hamming từ một dãy ký tự toàn số 0 và có cùng chiều dài. Có nghĩa là số phần tử trong dãy ký tự không có giá trị không (0): đối với một dãy ký tự nhị phân (binary string), nó chỉ là số các ký tự có giá trị một (1), lấy ví dụ trọng số Hamming của dãy ký tự 11101 là 4.
Bitmap vs Array: Khi một trong hai container là một bitmap và vùng còn lại là một mảng động đã được sắp xếp, phấn giao có thể được tính toán rất nhanh chóng: ta lặp qua mảng động đã sắp xếp và xác minh sự tồn tại của từng số nguyên 16 bit trong vùng chứa bitmap. Kết quả được ghi ra một Container mảng. Phép hợp cũng hiệu quả: ta tạo một bản sao của bitmap và chỉ cần lặp lại trên mảng, thiết lập các bit tương ứng.

Mảng vs Mảng: Đối với sự phép hợp, nếu lượng số không quá 4096, chúng tôi sử dụng thuật toán hợp nhất giữa hai mảng. Ngược lại ta đặt các bit tương ứng với cả hai mảng trong một container bitmap. Sau đó, chúng tôi tính toán lượng số bằng bằng cách sử dụng fast instructions. Nếu lượng số không quá 4096, chúng tôi chuyển đổi container bitmap thành container mảng (xem Thuật toán 2)
Đối với phép giao, ta sử dụng phép merge đơn giản (tương tự như những gì được thực hiện trong merge sort) khi hai mảng có lượng số khác nhau dưới hệ số 64. Ngược lại ta sử dụng galloping intersections. Kết quả luôn được ghi vào container mới. Phương pháp Gallop Phi hiệu quả hơn phép merge thông thường khi một mảng (r) nhỏ hơn nhiều so với mảng khác (f) vì nó có thể bỏ qua nhiều phép so sánh. Bắt đầu từ phần đầu của cả hai mảng, nó chọn phần tiếp theo có sẵn số nguyên ri từ mảng nhỏ (r) và tìm kiếm một số nguyên ít nhất bằng fj lớn trong mảng lớn f trước tiên nhìn vào giá trị tiếp theo, sau đó tìm một giá trị xa hơn hai lần, v.v. Sau đó, chúng tôi sử dụng tìm kiếm nhị phân trong danh sách thứ hai để tìm giá trị đầu tiên lớn hơn hoặc bằng ri

Roaring Bitmap thì có thể thực hiện tính toán và trả về kết quả mà không cần tạo ra container mới. Với trường hợp tính phép hợp giữa 2 bitmap container, thì chỉ cần sửa trên 1 trong 2 bitmap container đó. Còn với trường hợp phép hợp giữa 1 mảng và 1 bitmap container thì có thể thực hiện trên bitmap container luôn. Khi tổng hợp nhiều bitmap, Roaring Bitmap sử dụng nhiều thuật toán tối ưu khác. Ví dụ: khi tính toán sự kết hợp của nhiều bitmap (ví dụ: hàng trăm bitmap), nó sẽ xác định vị trí tất cả các container có cùng một khóa (sử dụng
hàng đợi ưu tiên). Nếu một container như vậy là bitmap container, thì chúng ta có thể sao chép bitmap container này (nếu cần) và tính toán sự kết hợp của container này với tất cả các container tương ứng tại chỗ. Trong trường hợp này, việc tính toán lượng sốcó thể được thực hiện một lần ở cuối. Xem Thuật toán 4.

Hình a và b hiển thị số bit trung bình được Java’s BitSet sử dụng và ba kỹ thuật nén bitmap để lưu trữ một số nguyên trong một tập hợp. Trong các thử nghiệm này, bitmap Roaring chỉ yêu cầu 50% không gian lưu trữ so với Concise và 25% so với WAH trên bitmap thưa.
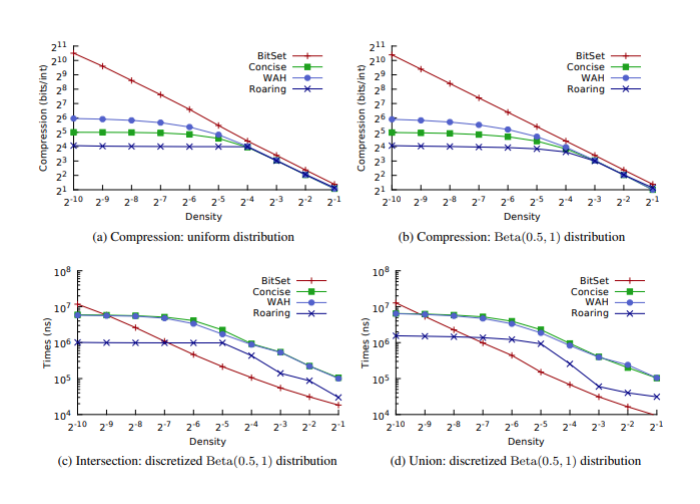
Đối với việc thực hiện phép giao và phép hợp thì trong ví dụ này ta lấy hai bitmap và tạo một bitmap mới đại diện cho phần giao hoặc phần hợp. Đối với BitSet, điều đó có nghĩa là trước tiên chúng ta cần để tạo một bản sao (sử dụng phương pháp sao chép), vì các thao tác với bit được thực hiện tại chỗ. Hình c và d biểu thị thời gian trung
bình tính bằng nano giây để thực hiện phép giao và hợp giữa hai tập hợp số nguyên.
Roaring Bitmap nhanh hơn 4 đến 5 lần so với Concise và WAH cho các phép giao trên tất cả các mật độ đã thử nghiệm. Kết quả cho các phép hợp cũng tương tự ngoại trừ rằng đối với mật độ vừa phải (2−5 ≤ d ≤ 2−4), Roaring chỉ nhanh hơn vừa phải là 30% so với Concise và WAH.
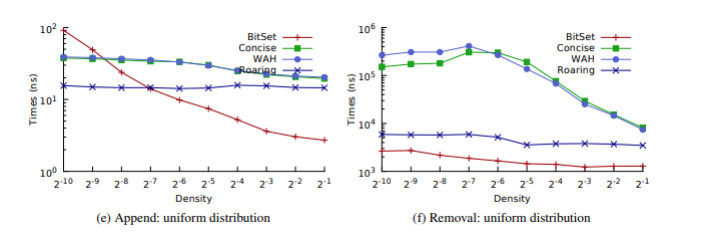
Thời gian đối với việc thêm một phần tử a vào một tập hợp S các số nguyên đã được sắp xếp, với ∀i ∈ S : a > i. Hình e cho thấy rằng Roaring cần ít thời gian hơn WAH và Concise. Hơn nữa, WAH và Concise không hỗ trợ việc chèn hiệu quả các giá trị theo thứ tự ngẫu nhiên, không giống như các Roaring Bitmap. Cuối cùng, Hình f biểu thị thời gian cần thiết để loại bỏ một phần tử được chọn ngẫu nhiên khỏi tập số nguyên. Kết quả là Roaring Bitmap có kết quả tốt hơn nhiều so với hai định dạng nén khác.
Roaring Bitmap là một phương pháp nén bitmap tương đối mới có hiệu quả tốt hơn về cả tốc độ cũng như việc sử dụng bộ nhớ so với các giải thuật nén trước đó như là WAH, Consise… Khi mà dữ liệu được sắp xếp như là các bitmap cần lưu trữ các giá trị lớn liên tiếp (ví dụ với bộ wikileaks), các lựa chọn thay thế như Concise hoặc WAH sẽ cung cấp tỉ lệ nén tốt hơn. Tuy vậy kể cả như vậy Roaring vẫn có thể có tốc độ nhanh hơn. Hiện nay thì kể từ lúc Roaring Bitmap được giới thiệu thì rất nhiều hệ thống đã ứng dụng nó để cải thiện tốc độ truy xuất xử lý dữ liệu. Các hệ thống tiêu biểu có thể kể đến như là: Apache Lucene với các hệ thống dẫn xuất của nó Solr and Elasticsearch, Apache Druid, Apache Spark, Apache Hive. . . Thư viện Roaring Bitmap với thời điểm ban đầu chỉ có trên Java nhưng hiện tại đã nhiều phiên bản miễn phí trên ngôn ngữ lập trình khác như C++, C#, Python, D, Node/Javascript. . . Điều này là minh chứng cho tính hiệu quả của Roaring Bitmap cũng như hứa hẹn sự phát triển và ứng dụng mạnh hơn nữa của nó trong các phần mềm tương lai.
Tài liệu tham khảo
Ngoài việc tham khảo nội dung trực tiếp từ trang https://roaringbitmap.org/ bài viết còn được tham khảo từ các nội dung sau:
[1] Oracle. “https://docs.oracle.com/cd/A8104201/DOC/server.816/a76994/indexes.htm”.
[2] Papakonstantinou Steven Swanson Jianguo Wang Chunbin Lin Yannis. “An Experimental Study of Bitmap
Compression vs. Inverted List Compression” (2017).
[3] Roberto Di Pietro Alessandro Colantonio. “Concise: Compressed ’n’ Composable Integer Set” (2010).
[4] O. Kaser R. Godin S. Chambi D. Lemire. “Better bitmap performance with Roaring bitmaps” (2016).
Bình luận: